高木浩光＠自宅の日記

■ アンチコリジョン機能のないRFIDタグの個数を調べる方法例

11月3日のアンチコリジョン機構がなければ紙幣にRFIDを付けても安全？で、

そのためには事実が知らされなくてはならない。IDが読めないことは関係がない。枚数を推定できるのかできないのかだ。そういう調査をしたという話は未だ聞いたことがない。

と書いたことに対して、

なんか相変わらず「とんでも」な事書いてるなぁ。 IDは読めないにしても、そこに何枚あるかがもし読み取られる状況であれば、って、なぜアンチコリジョン機構が必要か理解しているとは思えない記述。

少し検討してみよう。方式にもよるかもしれないが、基本的にはIDのビット列が異なる部分が衝突として検出されるはずである。（略）

例えば、128ビットの2つのIDのうち、 10ビットくらい違っていることは普通にありそうだ。 2^10=1024だから、普通の人は2千円〜1,024万円持っている可能性があることになる。実際に今持っているお札の数字をビット列にして、ビットが異なる数を検出したところ、 6個であった。さて私はいくら持っているだろうか？

調査なんぞしなくても、ちょっと考えてみれば済むことだ。衝突の話は、ブロッキング・タグの話が出てきた時に、ちゃんと読んでいればそういったことも分かるはずだ。

藝夢日報, アンチコリジョン機構を持たないIDタグの個数推定問題

などと書いている人がいると、11月3日のコメント欄で教えていただいた。

11月3日のコメントにも書いたように、デジタル化された後の話だけしても意味がない。アナログ信号レベルまで含めて何かできやしないかを確認する必要がある。一般に、セキュリティとは、すぐに思いつく正攻法の1つを否定して安心してよいという性質のものではない。そういう発想でセキュリティに関わる物を作ることは危険だ。

アナログ信号レベルで個数を推定する方法について、11月3日のコメント欄では、どのデジタル変調方式でも有効な、搬送波の位相のずれを測定する方法を挙げたが、そうした精密測定をしなくても、変調方式によってはもっと簡単な装置で推定する方法が有効である可能性があるので以下に書いておく。

位相のずれが搬送波の波長に比べて十分に短い（複数のタグからの距離の差が十分に小さく、応答のタイミングの個体差が十分に小さい）と仮定すると、複数のタグからの応答電波はリーダでは合成波として観測され、信号のデジタル変調方式がASKであるとすると、アナログ復調後の各ビットの重ね合わせは電位差として観測される。

（話を簡単にするためマンチェスタなどの変調符号のことを無視すると、）例えば 8ビットのランダムなビットパターンを応答するタグが2つあるとき、その重ね合わせは、

     10101001
     11000011
     --------
     21101012

などとなり、電位は最大のものに比して 100%, 50%, 50%, 0%, 50%, 0%, 50%, 100%となる。電位の数が3種類あることから、少なくとも2つのタグが存在することがわかる。

タグの数が増えると、0% や 100% などの極端な電位となるビット位置の存在確率が小さくなっていき、50% 前後の電位が多くなっていく。8ビットのタグが100個ある場合は、ほとんどのビット位置の電位が 50% 前後となるだろう。

では、128ビットのRFIDタグが30個存在する場合ではどうか。n通り以上の電位が現れる確率の計算式を求めればよいのだが、面倒なので、シミュレーションで確かめてみる。以下のRubyプログラムは、128ビットの乱数を32個生成して、各ビット位置ごとに1の数を合計し、合計数の集合を求めて、その要素の数を出力する。

num_of_tags = 30
num_of_bits = 128
srand
tags = []
for i in 0..(num_of_tags - 1)
    tags << rand(2 ** num_of_bits)
end
counters = []
for b in 0..(num_of_bits - 1)
    counters[b] = 0
    for i in 0..(num_of_tags - 1)
        if tags[i] % 2 == 1
            counters[b] += 1
        end
        tags[i] /= 2
    end
end
num = []
counters.each do |c|
    printf("%d ", c)
    num |= [c]
end
print "\n"
printf("%d\n", num.size)

これを25回試してみたところ次の結果となった。

19 15 21 19 16 14 15 14 15 15 16 17 15 14 14 15 13 14 14 13 14 15 15 15 15

これは、15種類前後の電位が観測されることを意味する。

タグの個数 n を変えながら試してみると、

n:
1: 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2: 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3: 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
4: 5 5 5 5 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
5: 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6
6: 7 7 7 7 7 7 7 6 6 6 7 7 7 7 7 7 7 7 7 7 6 7 7 7 5
7: 8 8 8 8 7 7 7 7 8 8 7 7 8 8 8 8 7 8 7 6 8 8 8 8 8
8: 8 9 8 7 7 7 8 8 7 8 8 7 9 8 8 7 8 9 8 7 7 7 8 8 8
9: 8 9 8 8 10 8 9 7 9 8 8 9 8 9 9 8 9 8 9 8 8 8 8 8 9
10: 7 9 9 8 8 9 8 9 8 9 9 9 10 8 9 8 10 9 9 9 9 10 9 7 8
11: 9 10 9 10 9 10 10 10 9 9 9 9 10 9 8 8 9 9 10 10 9 9 9 8 9
12: 9 11 10 9 8 11 9 11 10 9 8 10 10 11 9 9 8 11 10 10 10 9 9 10 7
13: 10 10 10 10 10 8 9 9 10 9 11 8 9 11 8 9 10 10 10 9 10 10 9 10 10
14: 11 11 10 10 11 9 9 9 10 9 10 9 10 10 10 10 12 12 10 10 10 9 11 9 9
15: 11 12 11 11 12 10 12 11 11 11 11 10 8 12 10 10 9 12 10 11 12 10 9 10 10
16: 9 11 9 11 11 11 12 10 12 10 9 11 10 10 9 11 11 10 10 11 12 12 11 11 11
17: 13 11 10 10 9 11 12 11 11 11 10 10 11 11 12 13 11 10 10 11 12 11 13 12 12
18: 11 11 11 10 11 12 11 12 13 11 13 10 12 11 11 11 13 11 9 12 13 12 12 12 11
19: 12 11 12 13 12 12 11 12 10 13 13 11 13 11 12 11 12 12 11 12 13 12 12 11 11
20: 12 12 13 13 13 12 13 11 13 12 12 12 12 11 11 12 12 11 11 11 11 11 13 12 12
21: 13 11 12 11 12 13 13 11 12 11 14 12 11 12 12 13 12 13 12 11 13 13 11 12 12
22: 11 12 14 12 13 13 12 13 14 14 13 14 12 13 13 13 13 12 12 11 12 12 14 13 11
23: 13 15 13 13 13 12 12 13 12 12 12 13 13 13 12 14 14 13 13 14 12 14 13 13 12
24: 11 12 12 13 14 13 12 12 14 11 12 14 13 14 12 12 14 13 12 11 12 12 13 12 14
25: 13 13 13 13 14 13 13 13 13 13 13 13 13 16 13 13 14 13 12 14 13 14 13 14 12
26: 13 13 13 13 14 14 14 15 15 14 12 13 13 14 14 13 15 12 13 12 15 14 12 13 13
27: 15 14 12 14 15 12 13 13 13 13 15 14 14 15 13 15 14 12 14 12 14 13 13 12 15
28: 14 14 15 14 14 14 13 15 14 14 12 16 13 13 12 14 13 15 16 13 13 15 13 15 13
29: 13 13 14 14 15 13 15 13 15 14 15 14 14 15 16 13 14 14 14 15 13 15 14 13 15
30: 14 14 16 13 14 13 15 14 14 14 14 14 13 15 15 15 14 15 12 13 14 13 13 16 14
31: 16 14 14 14 16 16 15 16 13 13 14 14 13 13 13 14 15 13 16 17 14 12 14 16 13
32: 14 13 15 15 17 15 15 15 15 13 15 15 16 14 11 17 13 13 13 16 17 16 15 15 14
33: 15 15 15 17 14 14 14 14 17 14 14 15 14 15 14 15 18 16 14 15 15 18 14 15 14
34: 16 17 15 15 16 16 14 17 16 15 15 16 15 15 14 15 15 16 16 13 15 15 17 13 16
35: 16 14 16 15 15 14 15 15 16 15 18 15 17 14 17 15 15 15 16 15 14 16 16 15 17
36: 15 17 16 14 15 14 18 12 16 15 16 16 15 15 16 14 15 14 15 16 16 15 14 16 17
37: 16 17 16 15 14 16 16 16 13 16 16 19 15 17 15 17 14 16 14 14 18 15 13 16 15
38: 17 17 16 17 16 16 15 16 18 16 14 16 18 16 11 17 17 17 17 17 15 14 17 17 17
39: 15 17 16 14 17 18 14 15 17 17 19 16 14 16 16 17 18 17 15 15 17 14 16 16 16
40: 16 17 16 16 14 15 16 15 17 16 18 16 16 17 18 16 17 17 15 17 17 18 16 15 15
41: 14 18 17 19 18 15 16 16 16 15 17 17 16 13 16 17 18 17 14 16 16 16 18 16 16
42: 16 16 15 18 17 17 17 14 17 13 17 19 16 16 18 15 16 17 15 16 17 14 17 14 17
43: 15 16 15 19 18 13 15 17 14 20 17 16 16 14 18 16 15 19 16 15 17 14 19 17 16
44: 17 17 19 15 16 16 16 20 18 18 19 16 17 18 17 17 17 17 18 16 16 17 16 18 19
45: 19 16 18 16 18 18 16 17 16 18 16 18 18 16 17 18 17 14 17 16 15 15 16 17 15
46: 16 18 17 19 19 19 17 17 17 16 17 19 17 17 16 17 15 18 16 19 16 17 20 16 18
47: 18 16 17 18 16 19 17 17 14 19 19 17 17 19 18 18 18 20 17 18 19 17 16 18 16
48: 19 16 19 18 14 17 18 17 16 15 17 18 19 17 16 19 17 15 17 17 17 17 18 17 16
49: 19 15 17 19 18 17 17 19 17 19 16 18 17 19 18 16 19 17 17 19 17 19 17 16 18
50: 17 16 17 18 18 15 18 17 17 18 17 18 17 19 17 18 19 18 20 15 18 17 19 19 17
51: 19 17 17 17 18 17 17 19 16 17 16 18 16 16 17 16 17 18 19 17 17 17 19 18 17
52: 19 16 17 19 19 18 18 17 17 20 20 17 16 16 20 20 17 18 17 20 15 18 18 17 17
53: 17 18 17 17 18 17 16 17 18 20 19 17 18 17 17 18 17 17 19 17 20 19 20 19 17
54: 21 19 18 18 18 18 19 18 17 21 19 17 19 17 18 19 18 20 18 17 20 17 19 17 17
55: 18 20 17 19 17 17 19 17 19 19 19 18 20 17 21 17 19 18 20 16 18 19 20 17 19
56: 19 19 19 15 18 19 18 19 18 21 15 18 17 19 21 21 15 19 18 17 17 19 20 19 19
57: 20 17 18 20 19 18 22 20 18 18 19 18 19 18 21 16 17 19 18 17 17 20 19 21 20
58: 20 19 18 19 18 21 17 19 21 18 19 18 16 19 15 20 19 21 18 17 18 21 17 20 20
59: 19 19 20 20 19 20 15 19 20 20 19 21 18 21 18 18 19 20 17 19 22 18 19 17 22
60: 20 19 17 18 20 19 18 18 16 20 19 20 18 19 19 19 19 21 17 21 19 22 20 19 19

となった。

10個あたりまではおおむねの数を推定できることがわかる。25個くらいまでなら±数個の誤差で推定できるようだ。15種類の電位が計測されたときは、26個くらい以上があるらしいと判断できる。

以下は、波形を図にしてみたものだ。上の図はタグが30個の場合で、下の図は10個の場合である。10個と30個とでは、違いを検出する装置を作れそうに思える。

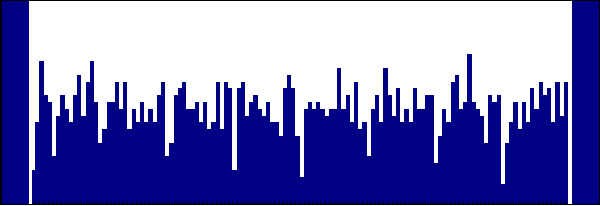
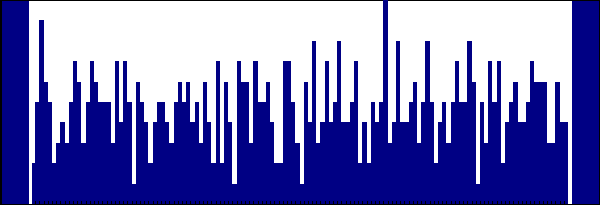
電位の数ではなく電位の絶対値（コリジョンのない信号部分の電位に対する比の値）から量子化ステップ数を求めて、タグの数を推定することもできるかもしれない。ただ、それは精密な解像度で電位を計測できるとの仮定が必要なので、上では同じ電位を示す数からおおまかに推定する方法を考えてみた。

電位の数を測定するにしても、測定精度の問題で、いくつまでを区別できるかはわからない。例えば、30段階に区別するのは難しいのかもしれない。

こうしたことができないことを確かめる必要があることを、11月3日の日記では述べた。